Month: December 2012

Let me apologize in advance for the brevity of today’s post.  You’ll see very shortly that I’ve been a bit under the weather the last few days.  It’s the very fact that I’ve been on and off bedridden with fever that got me to thinking about temperature and thermometers.

Specifically, I’ve been wondering how accurate any readings of my temperature have been.

Over the course of an hour or so (I’ve been a bit bored), I took thirty measurements of my temperature to see just how much any one of those measurements got it right.

Let’s cut to the chase, shall we?

 
To go back to last week, the mean and median are both 100.8, and the mode is 100.7.  The standard deviation, or the average amount that any given measurement deviates from the mean, is around .6. 

That means that the 95% confidence interval around my presumed actual temperature of somewhere around 100.8 is actually 99.6 to 102.0!

So, I guess my thermometer could be a bit more accurate.  In fact, it’s really quite poor.  

You are the first three contestants on The Price is Right!

Hopefully you can hear The Price is Right theme in your head the moment you see those words.  If you can’t, Google it.  Or call in sick tomorrow and watch some daytime TV.

Today we’re talking about the holding pit of The Price is Right – Contestants’ Row.

After my last post about The Price is Right a friend called me out on the fact that I could just watch a whole bunch of The Price is Right episodes and code them to pick up on the human behavior side.  I tried to dodge that idea a bit by explaining that I felt that there was a lot to learn – through simulation – about the situations the humans on the show find themselves in.

All said I knew that he was right – at some point I was going to have to sit down and code a bunch of The Price is Right Episodes.  I set my DVR to record every new episode in the series and before I knew it I had plenty of episodes to pull data from.

There are a lot of games on The Price is Right that have things that are difficult to code, and there are also games that are so infrequent as to be very difficult to code in any reasonable quantity.  For example, I’ve at the moment coded 15 episodes.  With six games on every show that means I’ve seen 90 pricing games.  Plinko has come up once.

I plan to keep coding episodes here and there to come back to some of the things that I simply need more data for.  After 15 episodes there should be something that I should be able to examine, though, right?

There are a few things that are constant on every show.  Every show has the Showcase Showdown at the end of the show.  Two individuals make bids on two showcases, which means that I’ve seen 30 showcase bids.

If you read my last post on The Wheel (or if you’ve ever seen The Price is Right ever) you know that twice a show three individuals have the chance to make two spins each, for 24 potential spins an episode.  That’s 360 potential spins, though a lot of those spins are highly interrelated.  It’s more fair to simply consider each set of three people as an event, leaving us with 30 wheel events.

The most abundant source of information across The Price is Right episodes is the information from Contestant’s Row.  Six times a show, four contestants each make a bid.  Again, these sets of bids are fairly interrelated, but that still leaves us with 90 sets of bids.

There’s a lot of information in these bids, and there’s a lot of potential things to look at.  After only a bit of thinking I realized that these bids would potentially make a great discussion about means, medians, and modes.  There’s more that I’ll get to, but if you’ve always struggled to remember these sorts of stats (or are teaching a stats class and can’t get it across to your students), hopefully this sort of practical example might help.

Now, before we get into it we should clarify exactly what happens during Contestants’ Row.  Four contestants are pulled from the audience and shown a prize.  The goal is to guess the price of the price, WITHOUT GOING OVER.  You can think of it like an auction.  You want to get the item for a deal, but you want to beat the other contestants that are also trying to get a deal.  The highest bid that still got the item for a deal (e.g. didn’t overpay) is the winner.

For example, if the bids on an item are 600, 700, 800, and 1000, and the price of the prize is 799, the contestant who bid 700 is the winner.  The contestants who bid 800 and 1000 were willing to pay too much, and the contestant who bid 700 was closer to the price than the contestant who bid 600.

If everyone bids over the price of the prize (e.g. if the price in the above example was 599), the bids reset and contestants start again.

Because of this, if a contestant thinks that all the other contestants have overbid they will frequently bid $1 – if they’re right in their assumption everyone else will be disqualified by being over the price and they will win.

When a contestant wins they leave Contestants’ Row and play a pricing game.  For the next bid their spot is filled with a new contestant, but the others remain the same.  The new contestant always get first bid, and bids move to the right (from the stage).

One of the main questions I had was about what the modal bid would be across all bids.  For those reading this for the stats review, the mode of a distribution is the number that is used the most frequently.  While a lot of numbers are used there is one that is used differently from all others.  That number is 1, the loneliest number.  So, is $1 the modal bid?  Let’s see.

[By the way, can anyone that works for Google and works on Google Docs get on adding histogram functionality to your spreadsheets?  It really can’t be that hard, right?  I love using Google Spreadsheets to make graphics, but not being able to make one of the most basic is a huge bummer.  They should be able to look like the graph below]

Well, you can see by that large spike at $1 that $1 bids are in fact the mode.  Of all 360 bids, 24 are $1 bids.  That might not seem like much (less than 10%), but the next most frequent bid is $800, with a frequency of 17.  After that it drops off pretty quick.

This is across all contestants, though, and there’s good reason to believe that dollar bids are more likely to come later in the chain of bidding.  If the first contestant bids $1 they run the risk of the second contestant bidding $2, effectively nullifying their bid.  That second contestant would run the risk of the third contestant bidding $3, who would also most certainly lose when the final contestant (hopefully!) bid $4.  So how does this look if we break it down by bid order?

As expected, almost all of the $1 bids are put in by the last contestant to bid.  A handful are placed by the third contestant to bid, but only 1 was placed by the second or first to bid.  You might be able to see that there are some $2 and $3 bids by the fourth contestant – these are in reaction to second and third contestants taking the dollar option away from them.

The mode of the fourth graph is very much $1, but the mode shifts out into the regular distribution for all earlier bidders.  The strength of the mode is much smaller in effect for the first three bidders – the mode for the first bidder is $1200, the mode for the third bidder is $600, and the mode for the second bidder is…multi-modal!

I feel like the second contestant spot just won $500 for a perfect bid.

What is multi-modal, you ask?  Well, when there’s no single mode, but several.  The most common case is bimodality, where two modes exist.  That actually happens to be the case here – $800 and $850 both occurred 5 times, and are each modes.  You can see though that a 5-frequency value being the mode is much less powerful than the 20:4 cut that occurs from $1 to the next best number for the fourth contestant.

So, not shockingly, $1 bids are used a lot – more than any other singular bid.  Those $1 bids are much more likely to occur later in the bidding process, and are non-existent in this sample for the first bidder.

Modes, got it?  Good.

If you’re familiar with making the above graphs you’ve likely noticed that I’ve removed the means from the sides – no use giving those away before it’s time.

Well, it’s time.  Means.  You can think of means as averages, because that’s what they are.  A mean is the sum of all values divided by the number of values.  If you had two values (please don’t use the mean of two values) that were 10 and 20, you can find the mean to be 15 by summing 10 and 20 (30), and then dividing by the number of values (2), which gives you 30/2 or 15.

So what’s the mean bid by contestant placement?

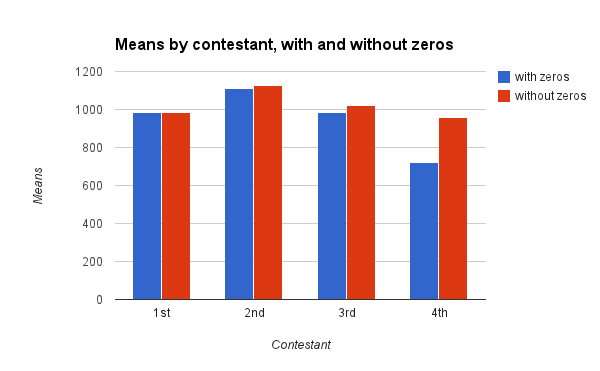
You can see that the mean drops quite a bit by the fourth contestant.  That drop is real, though it might not be meaningful.  Since the mean uses a sum of all numbers, having a whole bunch of numbers far outside the rest of the numbers will pull that mean – down, in this case.  How would the means look if we just took out all the $1 bids?

You can see pretty clearly that the mean is being pulled down by those $1 bids where those bids are more frequent – the most for the 4th contestant.

If means are being influenced, how about a different metric?

Medians are somewhat like means, except that instead of giving a straight average they give the value that is…well, medium?

If you have four friends and find yourself in the same room (or maybe in line at midnight to see a movie about Hobbits) with not much to talk about, line yourselves up by height.  The height of the person in the middle – the third person from either the top or bottom – is your median height.   

It doesn’t matter if you line up from shortest to tallest or tallest to shortest, and it doesn’t matter which side you count from.  It doesn’t matter what the height of the other people are – just the person in the middle.  You might have two friends that are an inch shorter than you and two friends and inch taller, or you might have two short friends and two NBA centers – it doesn’t matter.  All that matters is the height of the person in the middle.

Here’s what the median bids look like:

The medians are still being impacted (because 20 values are being removed from the forth contestant), but to a smaller degree.

All this is well and good, but these statistics are all pretty unimportant without context.  That context is the actual cost of the prizes being bid on.  The actual prices of prizes is a somewhat more interesting chart:

What is really interesting to notice is that there are no prizes – in the shows that I’ve watched – that are valued less than $500 (the lowest is $538).  There are also no prizes valued higher than $3000 (the highest is $2880).

Take note of that, contestants who bid $4500 on a regular basis.

The mean prize value is $1283.
The median prize value is $1195.
The modal prize value is…well, less important (it’s multi-modal and in the same range, though).

All said, it seems that $1 bids are somewhat unnecessary – a bit of $400 or $500 seems to serve the same purpose (though perhaps without the showmanship).  

It raises an interesting point, though.  Given the information so far, what values would you need to stay under to be confident to different levels that you’re not going to overbid?

Well, we can look at percentiles to get a feel for this.  Given the bids I’ve collected, a bid of $538 has an exceptionally low chance of being higher than the price of the prize.  What bid would be a bit higher but have a 95% chance of not going over?

$584.

Not a bad bid, it would seem.  You’re not going to go over, but you’re also likely to be a bit far from the actual price.

If you want to bump up your odds of winning at the cost of busting, you can be 75% confident in not going over with a bid of $811.  $800 is actually a pretty popular bid, so people might be picking up on this a bit.  There’s not a lot of situations where everyone goes over (it’s been once in the shows I’ve watched).

If you want to have a 50-50 shot at staying safe or going over your bid would be…well, I’ve already told you that.  Think about it for a minute before you read on, if you can’t come up with it.

The value of the 50th percentile is the median – $1195.

$1200 is also a pretty popular bid – especially for the first to bid.  

Want to run on the wild side a bit more?  A bid of $1761 gives you a 75% chance of being over the value of the prize.  A bid of $2276 gives you a 95% chance.

A bid of $4500?  Look, don’t do that.  Don’t do that, people.

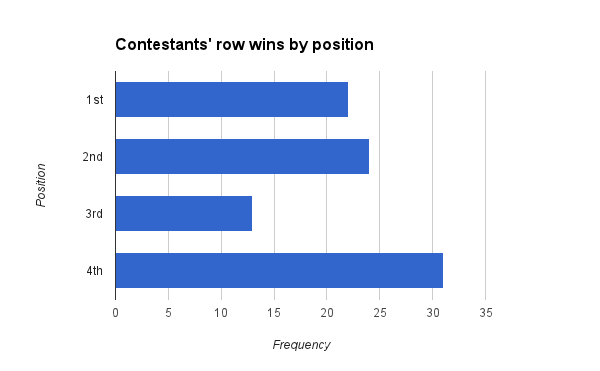
It does look like position had an impact on the sorts of bids that a contestant will make, so how does position impact your odds of winning?  Well, it’s actually pretty interesting.

The forth position seems to have a bit of an advantage.  More than that, the third position seems to have a bit of a disadvantage.  From a purely speculatory standpoint it does seem that the contestant first to bid often puts forth a pretty good bid fairly close to the actual price.  The second has the opportunity to bid fairly well, especially if the first hasn’t.  Good bids may be in short supply by the time it gets to the third contestant, and the third contestant also doesn’t yet have the advantage of the last bid.  If they bid $1 the forth position can easily bid $2.  If the third position bids one dollar more than the highest bid (also a good strategy), the forth still has the option of going one dollar higher.

So what’s the best bid?  Good question.  To a large degree it seems to be dependent pretty heavily on your position in the bidding order.  

If you do find yourself in Contestants’ Row the best advice might be to make sure to not bid $4500 without good cause.  Other than that, just play it smart and hope to find yourself in that forth spot.  Happy bidding! 

Well folks, you asked for it via vote.  Bad TV commercials.  Luckily there is no shortage.  

There is nothing that makes me lose respect for an actor or actress than when they get trapped in a series of commercials for a product and are basically the frontman (or woman) for a ridiculous campaign of misrepresentation.  If we’re making a list, Luke Wilson for AT&T would have to top it, but that’s already a few years gone.

The commercial that haunts my dreams at the moment is Jimmy Fallon and his awful 50% more cash commercials.

I’ve done a bit of research on this one to try to find out what some of the more popular credit cards are and how much the average person spends on different categories of goods, and came across a number of “independent studies” which have looked at what credit cards might be the best for people.  The problem is often that there is no one credit card that is the best for everyone, but the deeper problem is that almost all of these studies make claims based on what the data would look like for very specific people.

I don’t want to dwell too much on it, because it’s really a post in and of itself to debunk some of these pretty shoddy “studies”, but if you want to take a look for yourself they’re pretty easy to find with a quick Google search.

Back to the card at hand.  There’s a lot here, and it’s really easy to get bogged down in a whole lot of math and assumptions, so I’d like to keep things as concrete and objective as possible.  Let’s start here:

Okay, okay – you can say all you want that “oh, this is obviously a fake graph and it’s not important”, but let’s remember the bait and switch from earlier posts.  It’s really easy to say “who doesn’t like more cash?” – it’s actually the driving idea of the entire series of commercials: everyone likes more cash except the baby.

By the way, quick sidebar.  I hadn’t noticed it during the commercials, but check out the awesome child scientist working diligently in the background.  He’s wearing a lab coat because HE’S DOING SCIENCE.

So:
A) You like more cash.
B) The Capital One Cash Reward card can get you 50% more cash.
Hence: You like the Capital One Cash Reward card and should get one.

Again, there’s a reason why they don’t just have a chart that says “People Who Can Earn More Cash with the Capital One Cash Reward Card”, and it’s not just because it’s so long.  It’s because A) it would be a lot less than 100%, and B) they don’t want to actually do any research (the kid in the background is probably making ranch dressing).

The biggest trick here is that the Capital One Cash Reward card *CAN* get you 50% more cash.  Who can get 50% more cash?  People who are using credit cards that give 1% cash back.  Wait, there’s more.

This is from the Capital One website as of the writing of this post.  You see, there’s two versions of this card.  This should start to sound familiar: Jimmy Fallon isn’t talking to you unless you currently have a card that gives 1% cash back AND you have excellent credit.  If you simply have “average credit”, you can have your 50% more cash, but you also have to give Capital One $39 a year to do it.  Who has “average credit” you ask?  Probably the average person, and probably the kind of person who takes financial advice from Jimmy Fallon and a baby.   

With cash earning of 1% + 50% more cash, the first $2600 you spend on the card in any given year is just to cover the $39 fee.  What this means at a deeper level is that your rewards for using this card are actually variable, based on the amount spent in any given year. 

This graph takes into account those who apply for this card but don’t make it into the “excellent credit” category and end up with the “average credit” card, complete with $39 fee.  You can see that no person using this card will ever get to the level of 1.5%, as the graph is a simple asymptote right at that value.

Keep in mind, this is not how much you make in a year, but rather how much you spend on this credit card each year.  You hopefully spend less money using credit than what you make in any year, but I suppose it could also go the other way.
 
There’s another important point here in that Capital One is throwing around 50% a lot.  Why?  Because it sounds a lot better than 1.5%.  It’s very easy to make things sound better when you start talking about percents of percents, and it’s something to watch out for.

Anyway, the above is the worst case scenario.  Let’s say you have excellent credit and end up with the other card.  What are some of your options that could serve you better? 
 
Before I move to comparisons, there’s something else really useful to point out here.  All of the sites I went to that ranked cards using important research had links to those cards.  Surprise – those links went through affiliate sites and earned that referring site some nice cash (50% more, perhaps).  So, if you find a site that recommends a card but it seems like it might not actually be the best you might begin to wonder to yourself if that card is the best in other ways, such as affiliate referral payout. 

I’ve asked around a bit about what cards people use to get the best rewards, and there are a few that seem pretty common.  I’ll list out a few here for comparison.

Chase Freedom Card:
1% cash back on any purchases throughout the year, no cap
5% cash back on purchases in rotating rewards categories up to $1500 in purchases each quarter
10% cashback on online merchants through Chase
No annual fee

2012 Rotating Schedule:
Q1: Gas Stations, Amazon.com
Q2: Grocery Stores, Movie Theaters
Q3: Gas Stations, Restaurants
Q4: Hotels, Airlines, Best Buy, Kohl’s

If you have a Chase checking account, additionally:
10 points ($0.10 cash back) on every transaction, regardless of size
10% extra points (cash back) whenever points are earned

Chase Sapphire Card:
1% cash back on any purchases throughout the year, no cap
2% cash back on Dining
No annual fee

Discover More Card:
5% cash back on purchases in rotating rewards categories up to $1500 in purchases each quarter
1% back on everything else after you spend $3000 a year (not really worth factoring in)
No annual fee

2012 Rotating Schedule:
Q1: Gas Stations, Museums, Movies
Q2: Restaurants, Movies
Q3: Gas Stations, Theme Parks, Movies
Q4: Department Stores, All Online Shopping

Bank of America Cash Rewards Card (the 1-2-3 card):
1% cash back on any purchases throughout the year, no cap
2% cash back on groceries, up to $1500 in purchases each quarter (for groceries and gas combined)
3% cash back on gas stations, up to $1500 in purchases each quarter (for groceries and gas combined)
No annual fee

If you have a Bank of America account, additionally:
10% extra cash back whenever cash back is earned

I’m not telling you that you should have four credit cards (why would you only have four credit cards?), but you can see how you can easily pair up a few of these cards to put together a pretty all around 2-5% cash back system.  The Sapphire, for example, isn’t really good for anything other than restaurants, but if you only use it for restaurants you’re still earning 33% more cash back than the Capital One Cash Rewards Card (who likes 33% more cash?) – or, if you’re using Jimmy Fallon’s logic, 100% more cash back.

The Freedom and BoA cards are pretty strong, especially if you don’t mind opening up even a small account at one or both of them.  At that point you’re well above 1% with either card, so Jimmy Fallon is again no longer talking to you.  Discover is nice as a backup card to supplement categories that don’t match with other cards, or also good if you’re only using it and you hit that $3000 annual minimum.  Either way you’re again well above 1% cash back.  You’ll also be safe at all those places that only accept Discover.  Like…nowhere ever.

Looking through some cards online, it’s actually hard to find a card that simply gives 1% cash back.  You either run into these cards that give more than that (and well more than 50% more than that), or cards that don’t give cash back at all (including those that give less tangible rewards like airline points).  If you’re finding that you’re only eligible for credit cards that don’t give you anything back it might be time to revisit the notion that you need a credit card at this stage of your life.   

The bottom line is that the only way that you’re going to earn 50% more cash while using the Capital One Cash Rewards Card is if you’re DOING IT WRONG.

Turns out that the baby is actually the smartest person in the Capital One Cash Rewards Card commercials, even including the child scientist (who might be feeding Jimmy Fallon his poor research).

</rant>

There’s a point here, though.  While it’s not necessarily statistics (I promise I’ll get back to something much more statistical next week – you guys did request bad commercials), the use of percentages of percentages is probably the thing that gets under my skin here.  Of course it’s easy to give people 50% more of something if you’re not giving them much of it to begin with.  The base number is important, much more important than the ‘bonus’ percentage.

In fact, why stop at 50% more cash?  All you have to do is lower your regular rewards for this card to 0.75% instead of 1%, and then make the bonus 100% more cash instead of just 50% more cash.  Duh, who doesn’t want 100% more cash?  Probably that stupid baby, right?

Why stop at just 100%, though?  Make your standard reward 0.00015%, and then ask people if they want 1,000,000% more cash.  Who doesn’t want a million percent more cash?  Ugh. 

Should we go to scientific notation to really drive the point home?  Who wants 1e30% more cash?

Jimmy Fallon, please stop.  Just…stop.