On the Volatility of Distal Prediction or: Why I Get Speeding Tickets

So why can’t they just give us an answer?  Why can’t the weatherman tell us with certainty if it’s going to rain tomorrow?  Why can’t Yahoo just tell me how many points my lackluster running backs are going to fail to score this week?  Why can’t Blizzard or Valve tell us when their next game is going to hit stores?

Well, the short answer is that small deviations in a complex process can cause drastic and cascading fluctuations which themselves can cause drastic and cascading fluctuations.  That’s kind of the easy way out, though, so let’s talk about things in a way that makes this a bit more clear and simple.  

Speeding tickets.  

It’s been a few years since I’ve picked up a speeding ticket (I think there’s a very good possibility that I dodged one last week), but the place I seem to get them is on long trips.  Now, you could say that you get more tickets on longer trips because they’re longer, but unless you have a 4 hour daily commute I would argue that the ‘most car accidents happen within X minutes of your house’ logic holds here.  While long trips are longer, most of us don’t take them that often, and daily short trips add up quick.

So what makes my foot heavier on long trips?  Well, I can (for whatever reason) still remember the logic that was passing through my head on the trip where I received my first ticket, back in the summer of ’99.  

I tend to do a lot of math in my head when I’m driving.  It’s a good way to pass the time – I would highly recommend it.  The easiest and most pertinent math is estimates of travel time based on current and average speed.

The logic was somewhat like this.  I am currently traveling at 65 miles per hour.  This is a 5 hour trip.  If I go 5 miles per hour faster, that means that in the same time I’d go an extra 25 miles.  I don’t need to go an extra 25 miles, and since I’m doing a little better than a mile a minute that means that I would instead cut just under 25 minutes off the trip.  That’s worth it.  

Now, if it were to stop there, no problem.  As a math-hungry teenager you might easily see that it did not.  I am currently traveling at 70 miles per hour…

Anyway, I learned my lesson – to some degree – on that first ticket, and looking back at it it’s hard to believe how shocked I was that a cop would bother to stop me at my eventual speed.

That was long before GPS units and navigational capable phones were ubiquitous, so all the math had to be done in my head.  That probably slowed me down a bit, and if I had a GPS unit back then I wonder how fast I might have convinced myself was reasonable. 

You are almost certainly familiar with what I’m about to talk about if you’ve ever used constantly updating GPS navigation on a medium to long trip.  You put in the address, have it make up the route, and it pops up an estimated time of travel – often also an estimated time of arrival.  If you’re anything like me you look at that estimated arrival and round it down a little bit.  Most of the roads I travel on (i.e. every road I’ve ever traveled on) you tend to get run off the road if you’re simply doing the speed limit (which is usually what is used to calculate this estimate).  

I was on a drive last week that was actually somewhat similar in distance to the one I’ve described above from 13 years ago.  This time, though, I had GPS going throughout.  Boredom set in fast, and I started to do some math.  

The estimated time of arrival was longer than I knew the trip would take.  How much longer, though?  Could I figure out what my actual estimated arrival would be based on how fast I was changing it?

Without thinking about it too much I started paying attention to how many minutes of driving it took to drop the arrival estimate by a minute (e.g. from 6:30pm to 6:29pm).  My plan was to figure out how many minutes I saved with every minute of driving and then extrapolate out how many minutes I’d save over the minutes I had remaining in the trip.  I had done this for a while before I realized that the magnitude of the changes I was seeing was too tricky when measured at the minute level.  I either needed to go down to seconds and be more precise, or go up to hours to wash out some of that noise.

Let’s step back again for a second.  Why does your estimated arrival continue to change throughout the course of a trip?
   

Perhaps the best answer is that GPS navigation has yet to merge with Skynet, and doesn’t know how to learn.  Even after I’ve been driving a certain speed for several hours it still calculates time remaining based on the speed it thinks everyone is driving on any given road.  Maybe you’re asking yourself “if it doesn’t take into account your speed then how does the estimated arrival change at all?”

The calculation of time of arrival is based on a few things: distance, speed, and start time.  Imagine that your GPS only updated once during your trip, at the halfway point.  If you were going faster than expected in the first half of your trip, your estimated arrival will drop.  It’s not because the distance remaining or estimated speed has changed, but rather that you got to the halfway point earlier than you should have.  In effect, the start time for the second half of your trip has changed, and that’s what is changing your estimated arrival time.

GPS navigation (at least the ones I’m using) does not extrapolate from trends in data to prediction about future trends.  If it did, then the estimate of arrival time would be jumping around all over the place every time I sped up or slowed down.  Those of you with cars that do on-the-fly estimates of miles per gallon gas mileage know what this would look like.  In the case of estimated arrival time it’s probably prudent to make bets on a safe number (like estimated speed for the road) rather than current speed.  Imagine slowing down or stopping for road construction zone and having your estimated arrival suddenly jump to three weeks from now.     

Anyway, maybe it’s time to just make things a bit more concrete, right?

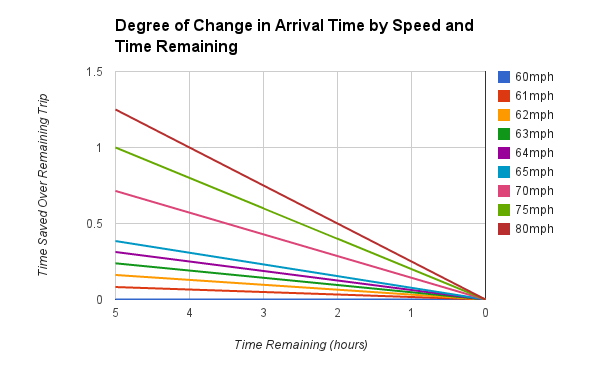
Let’s say that you were driving from Chicago to Orlando.  Google maps lets us know that it’s right around a 20 hour trip, and based on the distance and time it seems that the average speed that they’re estimating is right around 60 miles per hour.   How much time would you save if you drove the whole trip at 60mph?  Well, none.  It would take you around 20 hours.  How much time would you save by driving 61mph for that whole 20 hours?

Well, a single mph doesn’t buy you too much.  The gain per hour is only on the order of minutes.  It’s not until around 63mph over the course of the trip that you get yourself an hour back.  Still, driving 63mph instead of 60mph isn’t that bad, right?  To go back to my original example, 5mph over (65mph) gets you around an hour and a half back in your total trip.

Maybe you think 20 hours is too long of a trip – what does this look like on a shorter trip.  Well, pretty similar:

This actually matches with what I described before – on a five hour trip, going five miles an hour faster saves you a little less than 25 minutes.

Let’s just cut to the chase – how about going 20mph over the speed limit for the whole trip?  Well, on a five hour trip that saves you around an hour and 15 minutes.  On the 20 hour trip?  About 5 hours.  Crazy.

Now, I don’t want to just come out as if I’m saying that you should be doing 80mph on every 60mph road you come across.  What I’m saying is that the longer you have to cause a change, the larger change you can make with the same effort.

I’m also talking about average speeds.  These graphs take into account that you’re picking a speed and then sticking with it the rest of the trip.  If you start driving 80mph but then pull back a bit to 70mph or 60mph, or even something less than estimated (e.g. 55mph), the trend will work back toward the original estimate.

If you think about each of these lines as an estimate of error in the original 60mph based estimate you can also see that making estimates of your arrival time based on a 20 hour trip has a much wider range than if that trip was only an hour.

You can also see that the earlier you start making a change the larger impact it has.  If you want to save an hour on your 20 hour trip you simply need to drive around 63mph the whole time.  If you want to save that same hour from the last 5 hours of the same trip you need to do 75mph the whole time.  

There’s another way to look at it, as well.  Imagine that you wanted to average 65mph on your trip, and for simplicity’s sake there was no traffic.  If you’re just starting the 20 hour trip, you simply need to drive 65mph for every hour of the trip.

Say you forget to speed up in the beginning, though, and start the trip driving 60mph.  If you only drive 60mph for the first hour it doesn’t take much extra speed to compensate and get back to a 65mph average in the remaining 19 hours.  If you forget your plan for half the trip you’re in a little more trouble.  How much trouble?  Here’s a graph:

Halfway through, not that much trouble.  You simply need to drive 70mph for the rest of the trip.  Things really start to ramp up at the end – if you’ve made it to the last hour before realizing that you needed to average 65mph you need to do 160mph during that last hour of your trip.

There’s a Zeno’s paradox element to this in that you can see that this line is asymptotic.  The closer you get to your destination, the faster you need to go.  At a certain point this would break down from a practical standpoint given that a) your car (even assuming it’s really fast) can only accelerate so quickly in any given space, and b) the speed of light is a thing (even if skydivers regularly break it).   

How likely is it that you’re going to be able to pull off 160mph for that last hour?  Not very likely.  At the same time, how likely is it that you’d be able to pull of exactly 65mph for all 20 hours?  While more likely, it still has some problems.  At the start of that trip it’s really hard to say how fast you’ll be able to go, or even how fast you’ll want to go in a few hours.

Let’s step back for a second again.  Remember how GPS units calculate arrival estimates – the only thing that really changes is how fast you get to the next point that estimation occurs.  The closer and closer you get to the destination (in the above graphs the closer you get to the zero point on the right side), the narrower the error on the estimate of your arrival.  The reason is that imparting the same impact that you might have been able to make 19 hours prior with a speed change of 5mph now comes at a much greater cost.

The closer you get to an event the easier it is to predict because you have less time for error in prediction to accumulate.  

If we know that you’re likely to have an average speed somewhere between 60mph and 80mph we can now look at these above graphs as ranges of estimation.  If there is 5 hours left in the trip, the best you can do is really pick out a 75 minute window that you know you’ll arrive in.  At four hours your window closes a bit to an hour, and with only an hour remaining you should be able to estimate a 15 minute window in which you’ll arrive.

As a sidebar, this is also a good illustration of confidence intervals, but we’ll talk about that some other time.

Instead, imagine that someone else started the trip from the same place at the same time, that you each have a dozen or so different and differently reliable GPS units in each car and each of them only updates every week or so, and now you have a presidential race complete with polls.

That was supposed to be the punchline, but as I think about that last graph I think there’s actually another message there.  Imagine the difference between studying over the course of a week for a test, or pulling an all nighter.  Seems the message is pretty clear on that one, so I won’t belabor the point.

Of course, none of this should be used as an excuse for speeding unless you feel like explaining all of it to a cop to see if he buys it.  But – by all means – next time you’re in the car feel free to use this as an excuse to do a little math.